In this post I’ll cover how to run f4-statistics using the admixtools package for R. While I don’t typically use R for other tasks, I prefer this implementation over the original one because working in a REPL environment is more practical than editing parameter files, especially when you’re testing different population combinations. The interactive workflow makes programmatic model testing straightforward. Beyond these workflow improvements, the R version is also significantly faster, not due to any inherent language advantage, but simply better implementation. You can work with the full AADR dataset without creating subsets.
Setting Up R and Admixtools
First, install R and the required dependencies. For Ubuntu/Debian:
sudo apt update -y
sudo apt install -y r-base r-base-dev build-essential \
libcurl4-openssl-dev libssl-dev libxml2-dev libgsl-dev
Next, start R by running R in your terminal, then install admixtools:
install.packages("remotes")
remotes::install_github("uqrmaie1/admixtools")
What are f4-statistics?
F4-statistics measure genetic relationships between four populations by computing the average of (a-b)*(c-d) across SNPs, where a, b, c, d are allele frequencies in populations A, B, C, D respectively. They test whether allele frequency patterns are consistent with a simple tree topology, or whether they show evidence of admixture or differential relatedness between specific population pairs.
The statistic is written as F4(A, B; C, D), and under a simple tree model with no admixture, this value should be zero. In practice, the observed value is never exactly zero due to variation, which is why we use z-scores to assess statistical significance rather than expecting literal zeros.
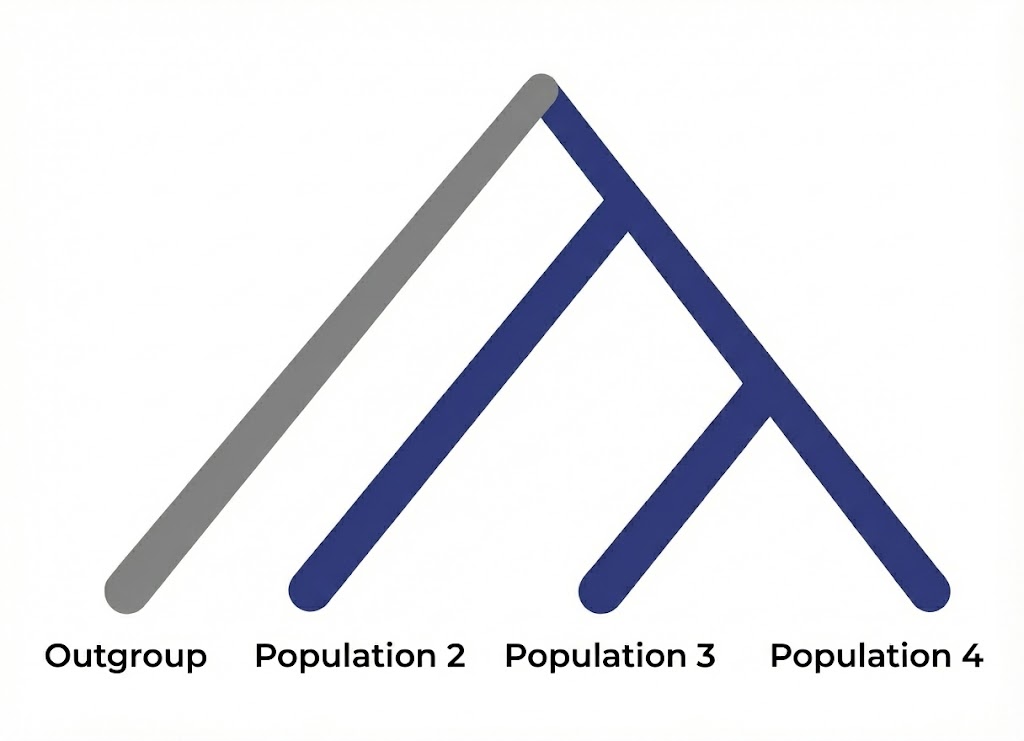
This is because any drift that affects the (A, B) branch should be independent of drift on the (C, D) branch. When F4 significantly deviates from zero, it indicates that the four populations don’t fit a simple tree, usually because of gene flow between populations that shouldn’t be connected under the assumed topology.
This might sound more complicated than it is. The key insight is that you’re testing whether populations form a simple tree or show signs of admixture. What happens under the hood (the actual computation) isn’t necessary to understand the practical use.
Running f4-statistics
I’ll use the AADR dataset, the most comprehensive curated collection of ancient and modern genomic samples. Since Admixtools works with EIGENSTRAT files and AADR is distributed in this format, the dataset can be used directly without preprocessing. For download instructions, see: Download Ancient & Modern DNA (AADR Tutorial).
Next, navigate to the directory containing your downloaded AADR dataset files (.geno, .snp, .ind) and start R:
cd /path/to/aadr/dataset
R
Load the previously installed admixtools library and dataset:
library(admixtools)
# Specify the file prefix (without extensions)
# If your files are named v62.0_HO_public.geno/.snp/.ind
# use only the prefix:
data = "v62.0_HO_public"
When specifying populations in f4-statistics, use the exact population labels from the third column of your .ind file, the function will automatically include all samples assigned to that population label.
Now we can run f4-statistics. You’ll need specific hypotheses about population relationships to test. I’ll demonstrate three examples that illustrate different outcomes.
In the examples below, pop1 through pop4 correspond to populations A, B, C, and D respectively, where (A, B) and (C, D) form the two pairs being compared.
Example 1: Do Yamnaya Share More Drift with EHG than WHG?
For this test, we’ll use Mbuti as the outgroup (position A), Yamnaya in position B, and EHG and WHG in positions C and D respectively. Note that positions within pairs (A,B) and (C,D) are interchangeable.
f4(data, pop1="Mbuti.HO", pop2="Russia_Samara_EBA_Yamnaya.AG", pop3="Italy_Epigravettian_alt.AG.BY.AA", pop4="Latvia_Mesolithic_oEHG.AG")
The result shows:
pop1 pop2 pop3 pop4 est se z p n
<chr> <chr> <chr> <chr> <dbl> <dbl> <dbl> <dbl> <dbl>
1 Mbuti.HO Russia_Samara_EBA_Ya… Ital… Latv… 0.00245 9.17e-4 2.67 0.00751 49477
The z-score of 2.67 falls just below the conventional significance threshold of 3, but the result is still informative. While some use a stricter threshold of |z| > 3, others consider |z| > 2 sufficient for exploratory analysis, particularly when the direction of the effect is theoretically motivated. The positive value indicates that Yamnaya shares more drift with EHG than with the WHG sample from Villabruna.
A positive f4-statistic means population B shares more drift with population D (rather than C). The estimate (0.00245) and its standard error allow us to assess both the direction and magnitude of the relationship.
While f4-statistics help identify population relationships and admixture signals, they don’t quantify ancestry proportions. For that, you’d use methods like qpAdm, which builds on f4-statistics to estimate admixture coefficients. I will cover qpAdm in the next post.
Example 2: Do Anatolian Neolithic Farmers Share More Drift with Sardinians or French?
f4(data, pop1="Mbuti.HO", pop2="Turkey_Marmara_Barcin_N.AG", pop3="Sardinian.HO", pop4="French.HO")
The result shows:
pop1 pop2 pop3 pop4 est se z p n
<chr> <chr> <chr> <chr> <dbl> <dbl> <dbl> <dbl> <dbl>
1 Mbuti.HO Turkey_Marmara_Ba… Sard… Fren… -0.00233 1.25e-4 -18.6 2.49e-77 155527
This result is highly significant with a z-score of -18.6. The negative value indicates that Anatolian Neolithic farmers (population B) share significantly more drift with Sardinians (population C) than with the French (population D). This confirms that Sardinians retain the highest proportion of Neolithic farmer ancestry in Europe, while the French have additional ancestry sources that dilute the Neolithic signal.
It’s important to note that the interpretation of an f4-statistic depends entirely on the populations you choose. If we replaced Sardinians with Han Chinese, the result would again be highly significant and show strong drift sharing between Neolithic Farmers and the French, but this time it would reflect shared Western Eurasian ancestry at a much deeper time depth, rather than specifically Neolithic farmer ancestry.
Example 3: How Do French, Scottish, and Norwegians Relate to Each Other?
f4(data, pop1="Mbuti.HO", pop2="French.HO", pop3="Scottish.HO", pop4="Norwegian.HO")
The result shows:
pop1 pop2 pop3 pop4 est se z p n
<chr> <chr> <chr> <chr> <dbl> <dbl> <dbl> <dbl> <dbl>
1 Mbuti.DG French.HO Scottish.HO Norwegian.HO 1.92e-4 2.05e-4 0.941 0.347 155583
The f4-statistic is non-significant (z = 0.941), indicating that the French share equal amounts of drift with Scottish and Norwegian populations. This result is consistent with a simple tree topology where these three populations diverged without subsequent gene flow between specific pairs. In other words, their genetic relationships can be explained by shared ancestry and geographic distance, without requiring admixture events that would preferentially connect any two of them.
Conclusion
F4-statistics are excellent for detecting signals of admixture and differential relatedness, but be cautious about overinterpreting the results. A significant f4-statistic tells you that populations don’t fit a simple tree, but it doesn’t tell you the directionality of gene flow or the ancestry proportions involved. For that, you need qpAdm, which I’ll cover in the next post.